The wflow_sbm Model

Introduction

The soil part of wflow_sbm model has its roots in the topog_sbm model but has had considerable changes over time. topog_sbm is specifically designed to simulate fast runoff processes in small catchments while wflow_sbm can be applied more widely. The main differences are:

• The unsaturated zone can be split-up in different layers

• The addition of evapotranspiration losses

• The addition of a capilary rise

• Wflow routes water over a D8 network while topog uses an element network based on contour lines and trajectories.

The sections below describe the working of the model in more detail.

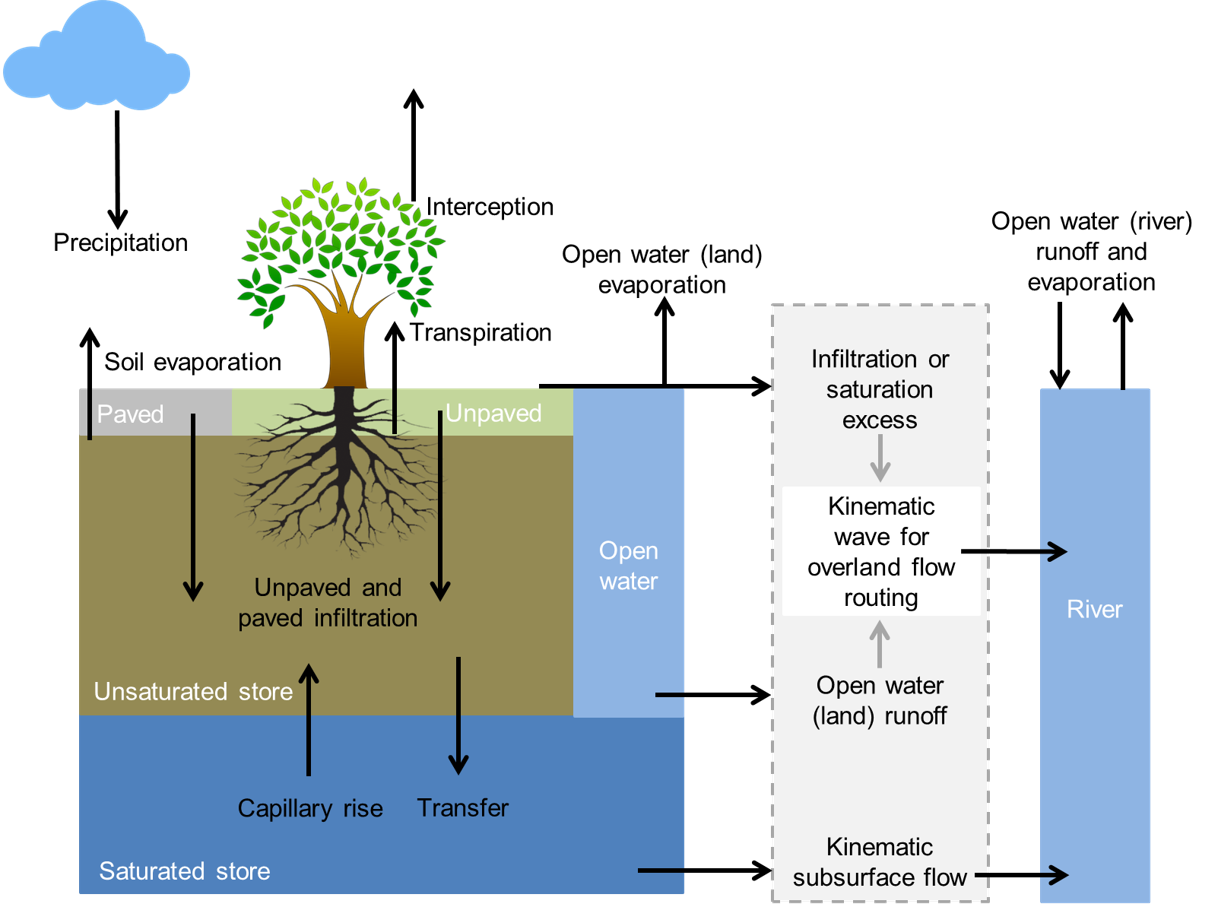
Overview of the different processes and fluxes in the wflow_sbm model.

Limitations

The wflow_sbm concept uses the kinematic wave approach for channel, overland and lateral subsurface flow, assuming that the topography controls water flow mostly. This assumption holds for steep terrain, but in less steep terrain the hydraulic gradient is likely not equal to the surface slope (subsurface flow), or pressure differences and inertial momentum cannot be neglected (channel and overland flow). In addition, while the kinemative wave equations are solved with a nonlinear scheme using Newton’s method (Chow, 1988), other model equations are solved through a simple explicit scheme. In summary the following limitations apply:

• Channel flow, and to a lesser degree overland flow, may be unrealistic in terrain that is not steep, and where pressure forces and inertial momentum are important.

• The lateral movement of subsurface flow may be very wrong in terrain that is not steep.

• The simple numerical solution means that results from a daily timestep model may be different from those with an hourly timestep.

Potential and Reference evaporation

The wflow_sbm model assumes the input to be potential evaporation. In many cases the evaporation will be a reference evaporation for a different land cover. In that case you can use the et_reftopot.tbl file to set the mutiplication per landuse to go from the supplied evaporation to the potential evaporation for each land cover. By default al is set to 1.0 assuming the evaporation to be potential.

Snow

Snow modelling is enabled by specifying the following in the ini file:

[model]
ModelSnow = 1

The snow model is described in the wflow_funcs Module Snow modelling

The snow model als has an optional (experimental) ‘mass-wasting’ routine. This transports snow downhill using the local drainage network. To use it set the variable MassWasting in the model section to 1.

# Masswasting of snow
# 5.67 = tan 80 graden
SnowFluxFrac = min(0.5,self.Slope/5.67) * min(1.0,self.DrySnow/MaxSnowPack)
MaxFlux = SnowFluxFrac * self.DrySnow
self.DrySnow = accucapacitystate(self.TopoLdd,self.DrySnow, MaxFlux)
self.FreeWater = accucapacitystate(self.TopoLdd,self.FreeWater,SnowFluxFrac * self.FreeWater )

Glaciers

Glacier processes are described in the wflow_funcs Module Glacier modelling

The rainfall interception model

This section is described in the wflow_funcs Module Rainfall Interception

The soil model

Infiltration

If the surface is (partly) saturated the throughfall and stemflow that falls onto the saturated area is added to the river runoff component (based on fraction rivers, self.RiverFrac) and to the overland runoff component (based on open water fraction (self.WaterFrac) minus self.RiverFrac). Infiltration of the remaining water is determined as follows:

The soil infiltration capacity can be adjusted in case the soil is frozen, this is optional and can be set in the ini file as follows:

[model]
soilInfRedu = 1

The remaining storage capacity of the unsaturated store is determined. The infiltrating water is split in two parts, the part that falls on compacted areas and the part that falls on non-compacted areas. The maximum amount of water that can infiltrate in these areas is calculated by taking the minimum of the maximum infiltration rate (InfiltCapsoil for non-compacted areas and InfiltCapPath for compacted areas) and the water on these areas. The water that can actual infiltrate is calculated by taking the minimum of the total maximum infiltration rate (compacted and non-compacted areas) and the remaining storage capacity.

Infiltration excess occurs when the infiltration capacity is smaller then the throughfall and stemflow rate. This amount of water (self.InfiltExcess) becomes overland flow (infiltration excess overland flow). Saturation excess occurs when the (upper) soil becomes saturated and water cannot infiltrate anymore. This amount of water (self.ExcessWater and self.ExfiltWater) becomes overland flow (saturation excess overland flow).

The wflow_sbm soil water accounting scheme

A detailed description of the Topog_SBM model has been given by Vertessy (1999). Briefly: the soil is considered as a bucket with a certain depth (\(z_{t}\)), divided into a saturated store (\(S\)) and an unsaturated store (\(U\)), the magnitudes of which are expressed in units of depth. The top of the \(S\) store forms a pseudo-water table at depth \(z_{i}\) such that the value of \(S\) at any time is given by:

\[S=(z_{t}-z_{i})(\theta_{s}-\theta_{r})\]

where:

\(\theta_{s}\) and \(\theta_{r}\) are the saturated and residual soil water contents, respectively.

The unsaturated store (\(U\)) is subdivided into storage (\(U_{s}\)) and deficit (\(U_{d}\)) which are again expressed in units of depth:

\[ \begin{align}\begin{aligned}U_{d}=(\theta_{s}-\theta_{r})z_{i}-U\\U_{s}=U-U_{d}\end{aligned}\end{align} \]

The saturation deficit (\(S_{d}\)) for the soil profile as a whole is defined as:

\[S_{d}=(\theta_{s}-\theta_{r})z_{t}-S\]

All infiltrating water enters the \(U\) store first. The unsaturated layer can be split-up in different layers, by providing the thickness [mm] of the layers in the ini file. The following example specifies three layers (from top to bottom) of 100, 300 and 800 mm:

[model]
UStoreLayerThickness = 100,300,800

The code checks for each grid cell the specified layers against the SoilThickness, and adds or removes (partly) layer(s) based on the SoilThickness.

Assuming a unit head gradient, the transfer of water (\(st\)) from a \(U\) store layer is controlled by the saturated hydraulic conductivity \(K_{sat}\) at depth \(z\) (bottom layer) or \(z_{i}\), the effective saturation degree of the layer, and a Brooks-Corey power coefficient (parameter \(c\)) based on the pore size distribution index \(\lambda\) (Brooks and Corey (1964)):

\[ \begin{align}\begin{aligned}st=K_{\mathit{sat}}\left(\frac{\theta-\theta_{r}}{\theta_{s}-\theta_{r}}\right)^{c}\\c=\frac{2+3\lambda}{\lambda}\end{aligned}\end{align} \]

When the unsaturated layer is not split-up into different layers, it is possible to use the original Topog_SBM vertical transfer formulation, by specifying in the ini file:

[model]
transfermethod = 1

The transfer of water from the \(U\) store to the \(S\) store (\(st\)) is in that case controlled by the saturated hydraulic conductivity \(K_{sat}\) at depth \(z_{i}\) and the ratio between \(U\) and \(S_{d}\):

\[st=K_{\mathit{sat}}\frac{U_{s}}{S_{d}}\]

Schematisation of the soil and the connection to the river within the wflow_sbm model

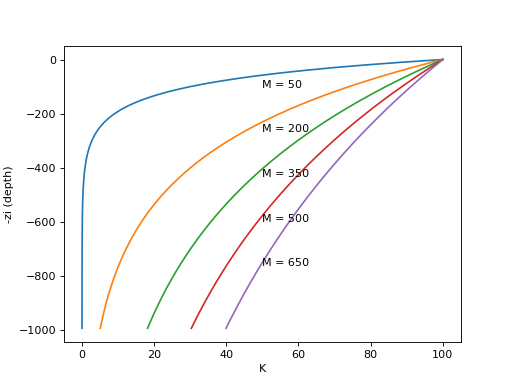
Saturated conductivity (\(K_{sat}\)) declines with soil depth (\(z\)) in the model according to:

\[K_{sat}=K_{0}e^{(-fz)}\]

where:

\(K_{0}\) is the saturated conductivity at the soil surface and

\(f\) is a scaling parameter [\(mm^{-1}\)]

The scaling parameter \(f\) is defined by:

\(f=\frac{\theta_{s}-\theta_{r}}{M}\)

with \(\theta_{s}\) and \(\theta_{r}\) as defined previously and \(M\) representing a model parameter (expressed in millimeter).

Figure: Plot of the relation between depth and conductivity for different values of M

(Source code, png, hires.png, pdf)

The kinematic wave approach for lateral subsurface flow is described in the wflow_funcs Module Subsurface flow routing

Transpiration and soil evaporation

The potential eveporation left over after interception and open water evaporation (rivers and water bodies) is split in potential soil evaporation and potential transpiration based on the canopy gap fraction (assumed to be identical to the amount of bare soil).

For the case of one single soil layer, soil evaporation is scaled according to:

\(soilevap = potensoilevap \frac{SaturationDeficit}{SoilWaterCapacity}\)

As such, evaporation will be potential if the soil is fully wetted and it decreases linear with increasing soil moisture deficit.

For more than one soil layer, soil evaporation is only provided from the upper soil layer (often 100 mm) and soil evaporation is split in evaporation from the unsaturated store and evaporation from the saturated store. First water is evaporated water from the unsaturated store. Then the remaining potential soil evaporation can be used for evaporation from the saturated store. This is only possible, when the water table is present in the upper soil layer (very wet conditions). Both the evaporation from the unsaturated store and the evaporation from the saturated store are limited by the minimum of the remaining potential soil evaporation and the available water in the unsaturated/saturated zone of the upper soil layer. Also for multiple soil layers, the evaporation (both unsaturated and saturated) decreases linearly with decreasing water availability.

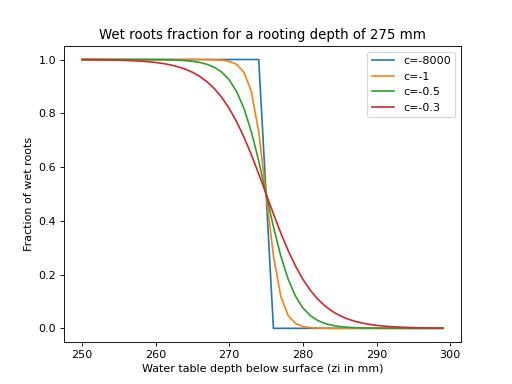
The original Topog_SBM model does not include transpiration or a notion of capilary rise. In wflow_sbm transpiration is first taken from the \(S\) store if the roots reach the water table \(z_{i}\). If the \(S\) store cannot satisfy the demand the \(U\) store is used next. First the number of wet roots is determined (going from 1 to 0) using a sigmoid function as follows:

\[WetRoots = 1.0/(1.0 + e^{-SharpNess (WaterTable - RootingDepth)})\]

Here the sharpness parameter (by default a large negative value, -80000.0) parameter determines if there is a stepwise output or a more gradual output (default is stepwise). WaterTable is the level of the water table in the grid cell in mm below the surface, RootingDepth is the maximum depth of the roots also in mm below the surface. For all values of WaterTable smaller that RootingDepth a value of 1 is returned if they are equal a value of 0.5 is returned if the WaterTable is larger than the RootingDepth a value of 0 is returned. The returned WetRoots fraction is multiplied by the potential evaporation (and limited by the available water in saturated zone) to get the transpiration from the saturated part of the soil:

# evaporation from saturated store
wetroots = _sCurve(dyn['zi'][idx], a=static['ActRootingDepth'][idx], c=static['rootdistpar'][idx])
dyn['ActEvapSat'][idx] = min(PotTrans * wetroots, dyn['SatWaterDepth'][idx])
dyn['SatWaterDepth'][idx] = dyn['SatWaterDepth'][idx] - dyn['ActEvapSat'][idx]
RestPotEvap = PotTrans - dyn['ActEvapSat'][idx]

Figure: Plot showing the fraction of wet roots for different values of c for a RootingDepth of 275 mm

(Source code, png, hires.png, pdf)

Next the remaining potential evaporation is used to extract water from the unsaturated store. The fraction of roots (AvailCap) that cover the unsaturated zone for each soil layer is used to calculate the potential root water extraction rate (MaxExtr):

MaxExtr = AvailCap * UstoreLayerDepth

When setting Whole_UST_Avail to 1 in the ini file as follows, the complete unsaturated storage is available for transpiration:

[model]
Whole_UST_Avail = 1

Next, the Feddes root water uptake reduction model (Feddes et al. (1978)) is used to calculate a reduction coefficient as a function of soil water pressure. Soil water pressure is calculated following Brooks and Corey (1964):

\[\frac{(\theta-\theta_r)}{(\theta_s-\theta_r)} = \Bigg\lbrace{\left(\frac{h_b}{h}\right)^{\lambda}, h > h_b \atop 1 , h \leq h_b}\]

where:

\(h\) is the pressure head (cm), \(h_b\) is the air entry pressure head, and \(\theta\), \(\theta_s\), \(\theta_r\) and \(\lambda\) as previously defined.

Feddes (1978) described a transpiration reduction-curve for the reduction coefficient \(\alpha\), as a function of \(h\). Below, the function used in wflow_sbm, that calculates actual transpiration from the unsaturated zone layer(s).

def actTransp_unsat_SBM(RootingDepth, UStoreLayerDepth, sumLayer, RestPotEvap, sumActEvapUStore, c, L,
thetaS, thetaR, hb, ust=0):

"""
Actual transpiration function for unsaturated zone:

  if ust is True, all ustore is available for transpiration

Input:

    - RootingDepth, UStoreLayerDepth, sumLayer (depth (z) of upper boundary unsaturated layer),
      RestPotEvap (remaining evaporation), sumActEvapUStore (cumulative actual transpiration (more than one UStore layers))
      c (Brooks-Corey coefficient), L (thickness of unsaturated zone), thetaS, thetaR, hb (air entry pressure), ust

Output:

    - UStoreLayerDepth,  sumActEvapUStore, ActEvapUStore
"""

# AvailCap is fraction of unsat zone containing roots
if ust >= 1:
    AvailCap = UStoreLayerDepth * 0.99
else:
    if L > 0:
        AvailCap = min(1.0, max(0.0, (RootingDepth - sumLayer) / L))
    else:
        AvailCap = 0.0

MaxExtr = AvailCap * UStoreLayerDepth

# Next step is to make use of the Feddes curve in order to decrease ActEvapUstore when soil moisture values
# occur above or below ideal plant growing conditions (see also Feddes et al., 1978). h1-h4 values are
# actually negative, but all values are made positive for simplicity.
h1 = hb  # cm (air entry pressure)
h2 = 100  # cm (pF 2 for field capacity)
h3 = 400  # cm (pF 3, critical pF value)
h4 = 15849  # cm (pF 4.2, wilting point)

# According to Brooks-Corey
par_lambda = 2 / (c - 3)
if L > 0.0:
    vwc = UStoreLayerDepth / L
else:
    vwc = 0.0
vwc = max(vwc, 0.0000001)
head = hb / (
    ((vwc) / (thetaS - thetaR)) ** (1 / par_lambda)
)  # Note that in the original formula, thetaR is extracted from vwc, but thetaR is not part of the numerical vwc calculation
head = max(head,hb)

# Transform h to a reduction coefficient value according to Feddes et al. (1978).
# For now: no reduction for head < h2 until following improvement (todo):
#       - reduction only applied to crops
if(head <= h1):
    alpha = 1
elif(head >= h4):
    alpha = 0
elif((head < h2) & (head > h1)):
    alpha = 1
elif((head > h3) & (head < h4)):
    alpha = 1 - (head - h3) / (h4 - h3)
else:
    alpha = 1

ActEvapUStore = (min(MaxExtr, RestPotEvap, UStoreLayerDepth)) * alpha

UStoreLayerDepth = UStoreLayerDepth - ActEvapUStore

RestPotEvap = RestPotEvap - ActEvapUStore
sumActEvapUStore = ActEvapUStore + sumActEvapUStore

return UStoreLayerDepth, sumActEvapUStore, RestPotEvap

Capilary rise is determined using the following approach: first the \(K_{sat}\) is determined at the water table \(z_{i}\); next a potential capilary rise is determined from the minimum of the \(K_{sat}\), the actual transpiration taken from the \(U\) store, the available water in the \(S\) store and the deficit of the \(U\) store. Finally the potential rise is scaled using the distance between the roots and the water table using:

\(CSF=CS/(CS+z_{i}-RT)\)

in which \(CSF\) is the scaling factor to multiply the potential rise with, \(CS\) is a model parameter (default = 100, use CapScale.tbl to set differently) and \(RT\) the rooting depth. If the roots reach the water table (\(RT>z_{i}\)) \(CS\) is set to zero thus setting the capilary rise to zero.

Leakage

If the MaxLeakage parameter is set > 0, water is lost from the saturated zone and runs out of the model.

Soil temperature

The near surface soil temperature is modelled using a simple equation (Wigmosta et al., 2009):

\[T_s^{t} = T_s^{t-1} + w (T_a - T_s^{t-1})\]

where \(T_s^{t}\) is the near-surface soil temperature at time t, \(T_a\) is air temperature and \(w\) is a weighting coefficient determined through calibration (default is 0.1125 for daily timesteps).

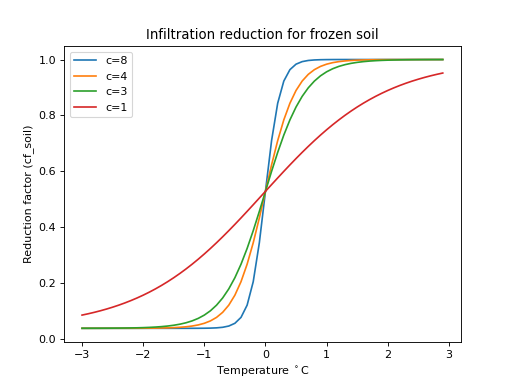
A reduction factor (cf_soil, default is 0.038) is applied to the maximum infiltration rate (InfiltCapSoil and InfiltCapPath), when the following model settings are specified in the ini file:

[model]
soilInfRedu = 1
ModelSnow = 1

A S-curve (see plot below) is used to make a smooth transition (a c-factor (c) of 8 is used):

\[\begin{split}b &= \frac{1.0}{(1.0 - cf\_soil)}\\ soilInfRedu &= \frac{1.0}{b + exp(-c (T_s - a))} + cf\_soil\\ a &= 0.0\\ c &= 8.0\end{split}\]

(Source code, png, hires.png, pdf)

Irrigation and water demand

Water demand (surface water only) by irrigation can be configured in two ways:

1. By specifying the water demand externally (as a lookup table, series of maps etc)

2. By defining irrigation areas. Within those areas the demand is calculated as the difference between potential ET and actual transpiration

For both options a fraction of the supplied water can be put back into the river at specified locations

The following maps and variables can be defined:

• wflow_irrigationareas.map: Map of areas where irrigation is applied. Each area has a unique id. The areas do not need to be continuous& but all cells with the same id are assumed to belong to the same irrigation area.

• wflow_irrisurfaceintake.map: Map of intake points at the river(s). The id of each point should correspond to the id of an area in the wflow_irrigationareas map.

• wflow_irrisurfacereturns.map: Map of water return points at the river(s). The id of each point should correspond to the id of an area in the wflow_irrigationareas map or/and the wflow_irrisurfaceintake.map.

• IrriDemandExternal: Irrigation demand supplied to the model. This can be doen by adding an entry to the modelparameters section. if this is doen the irrigation demand supplied here is used and it is NOT determined by the model. Water demand should be given with a negative sign! See below for and example entry in the modelparameters section:

  IrriDemandExternal=intbl/IrriDemandExternal.tbl,tbl,-34.0,0,staticmaps/wflow_irrisurfaceintakes.map
  

  In this example the default demand is -34 m\(^3\) s\(^{-1}\). The demand must be linked to the map wflow_irrisurfaceintakes.map. Alternatively we can define this as a timeseries of maps:

  IrriDemandExternal=/inmaps/IRD,timeseries,-34.0,0
  

• DemandReturnFlowFraction: Fraction of the supplied water the returns back into the river system (between 0 and 1). This fraction must be supplied at the wflow_irrisurfaceintakes.map locations but the water that is returned to the river will be returned at the wflow_irrisurfacereturns.map locations. If this variable is not defined the default is 0.0. See below for an example entry in the modelparameters section:

  DemandReturnFlowFraction=intbl/IrriDemandReturn.tbl,tbl,0.0,0,staticmaps/wflow_irrisurfaceintakes.map
  

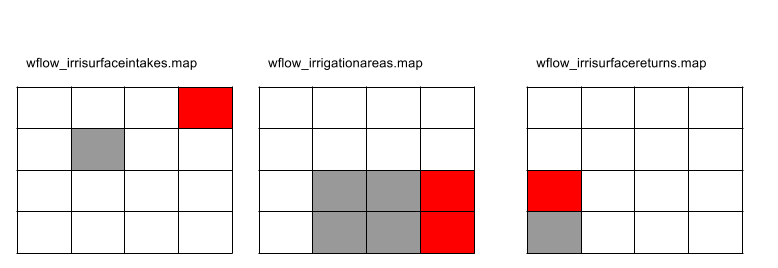
Figure showing the three maps that define the irrigation intake points areas and return flow locations.

The irrigation model can be used in the following two modes:

1. An external water demand is given (the user has specified the IrriDemandExternal variable). In this case the demand is enforced. If a matching irrigation area is found the supplied water is converted to an amount in mm over the irrigation area. The supply is converted in the next timestep as extra water available for infiltration in the irrigation area. If a DemandReturnFlowFraction is defined this fraction is the supply is returned to the river at the wflow_irrisurfacereturns.map points.

2. Irrigation areas have been defined and no IrriDemandExternal has been defined. In this case the model will estimate the irrigation water demand. The irrigation algorithim works as follows: For each of the areas the difference between potential transpiration and actual transpiration is determined. Next, this is converted to a demand in m\(^3\) s\(^{-1}\) at the corresponding intake point at the river. The demand is converted to a supply (taking into account the available water in the river) and converted to an amount in mm over the irrigation area. The supply is converted in the next timestep as extra water available for infiltration in the irrigation area. This option has only be tested in combination with a monthly LAI climatology as input. If a DemandReturnFlowFraction is defined this fraction is the supply is returned to the river at the wflow_irrisurfacereturns.map points.

Paddy areas and irrigation

Paddy areas (irrigated rice fields) can be defined by including the following maps:

• wflow_irrigationpaddyareas.map: Map of areas where irrigated rice fields are located.

• wflow_hmax.map: Map with the optimal water height [mm] in the irrigated rice fields.

• wflow_hp.map: Map of the water height [mm] when rice field starts spilling water (overflow).

• wflow_hmin.map: Map with the minimum required water height in the irrigated rice fields.

• wflow_irrisurfaceintake.map: Map of intake points at the river(s). The id of each point should correspond to the id of an area in the wflow_irrigationpaddyareas map.

Furthermore, gridded timeseries whether rice crop growth occurs (value = 1), or not (value = 0), are required. These timeseries can be included as follows:

[modelparameters]
CRPST=inmaps/CRPSTART,timeseries,0.0,1

Wflow_sbm will estimate the irrigation water demand as follows, a ponding depth (self.PondingDepth) is simulated in the grid cells with a rice crop. Potential evaporation left after interception and open water evaporation (self.RestEvap), is subtracted from the ponding depth as follows:

if self.nrpaddyirri > 0:
    self.ActEvapPond = pcr.min(self.PondingDepth, self.RestEvap)
    self.PondingDepth = self.PondingDepth - self.ActEvapPond
    self.RestEvap = self.RestEvap - self.ActEvapPond

Infiltration excess and saturation excess water are added to the ponding depth in grid cells with a rice crop, to the maximum water height when the rice field starts spilling water.

The irrigation depth is then determined as follows:

if self.nrpaddyirri > 0:
    irr_depth = (
        pcr.ifthenelse(
            self.PondingDepth < self.h_min, self.h_max - self.PondingDepth, 0.0
        )
        * self.CRPST
    )

The irrigation depth is converted to m\(^3\) s\(^{-1}\) for each irrigated paddy area, at the corresponding intake point at the river. The demand is converted to a supply (taking into account the available water in the river) and converted to an amount in mm over the irrigation area. The supply is converted in the next timestep as extra water available for infiltration in the irrigation area.

This functionality was added to simulate rice crop production when coupled (through Basic Model Interface (BMI)) to the The wflow_lintul Model.

Kinematic wave, Length, Width and Slope

Both overland flow and river flow are routed through the catchment using the kinematic wave equation. For overland flow, width (self.SW) and length (self.DL) characteristics are based on the grid cell dimensions and flow direction, and in case of a river cell, the river width is subtracted from the overland flow width. For river cells, both width and length can either be supplied by separate maps:

• wflow_riverwidth.map

• wflow_riverlength.map

or determined from the grid cell dimension and flow direction for river length and from the DEM, the upstream area and yearly average discharge for the river width (Finnegan et al., 2005):

The yearly average Q at outlet is scaled for each point in the drainage network with the upstream area. \(\alpha\) ranges from 5 to > 60. Here 5 is used for hardrock, large values are used for sediments.

When the river length is calculated based on grid dimensions and flow direction in wflow_sbm, it is possible to provide a map with factors to multiply the calculated river lenght with (wflow_riverlength_fact.map, default is 1.0).

The slope for kinematic overland flow and river flow can either be provided by maps:

• Slope.map (overland flow)

• RiverSlope.map (river flow)

or calculated by wflow_sbm based on the provided DEM and Slope function of PCRaster.

Note

If a river slope is available as map, then we recommend to also provide a river lenght map to avoid possible inconsistencies between datasets. If a river lenght map is not provided, the river length is calculated based on grid dimensions and flow direction, and if available the wflow_riverlength_fact.map.

Implementation of river width calculation:

if (self.nrresSimple + self.nrlake) > 0:
    upstr = pcr.catchmenttotal(1, self.TopoLddOrg)
else:
    upstr = pcr.catchmenttotal(1, self.TopoLdd)
Qscale = upstr / pcr.mapmaximum(upstr) * Qmax
W = (
    (alf * (alf + 2.0) ** (0.6666666667)) ** (0.375)
    * Qscale ** (0.375)
    * (pcr.max(0.0001, pcr.windowaverage(self.riverSlope, pcr.celllength() * 4.0)))
    ** (-0.1875)
    * self.NRiver ** (0.375)
)
# Use supplied riverwidth if possible, else calulate
self.RiverWidth = pcr.ifthenelse(self.RiverWidth <= 0.0, W, self.RiverWidth)

The table below list commonly used Manning’s N values (in the N_River.tbl file). Please note that the values for non river cells may arguably be set significantly higher. (Use N.tbl for non-river cells and N_River.tbl for river cells)

Manning’s N values

Type of Channel and Description	Minimum	Normal	Maximum
Main Channels
clean, straight, full stage, no rifts or deep pools	0.025	0.03	0.033
same as above, but more stones and weeds	0.03	0.035	0.04
clean, winding, some pools and shoals	0.033	0.04	0.045
same as above, but some weeds and stones	0.035	0.045	0.05
same as above, lower stages, more ineffective slopes and sections	0.04	0.048	0.055
same as second with more stones	0.045	0.05	0.06
sluggish reaches, weedy, deep pools	0.05	0.07	0.08
very weedy reaches, deep pools, or floodways with heavy stand of timber and underbrush	0.075	0.1	0.15
Mountain streams
bottom: gravels, cobbles, and few boulders	0.03	0.04	0.05
bottom: cobbles with large boulders	0.04	0.05	0.07

Natural lakes and reservoirs can also be added to the model and taken into account during the routing process. For more information, see the documentation of the wflow_funcs module.

Subcatchment flow

Normally the the kinematic wave is continuous throughout the model. By using the the SubCatchFlowOnly entry in the model section of the ini file all flow is at the subcatchment only and no flow is transferred from one subcatchment to another. This can be handy when connecting the result of the model to a water allocation model such as Ribasim.

Example:

[model]
SubCatchFlowOnly = 1

Model variables stores and fluxes

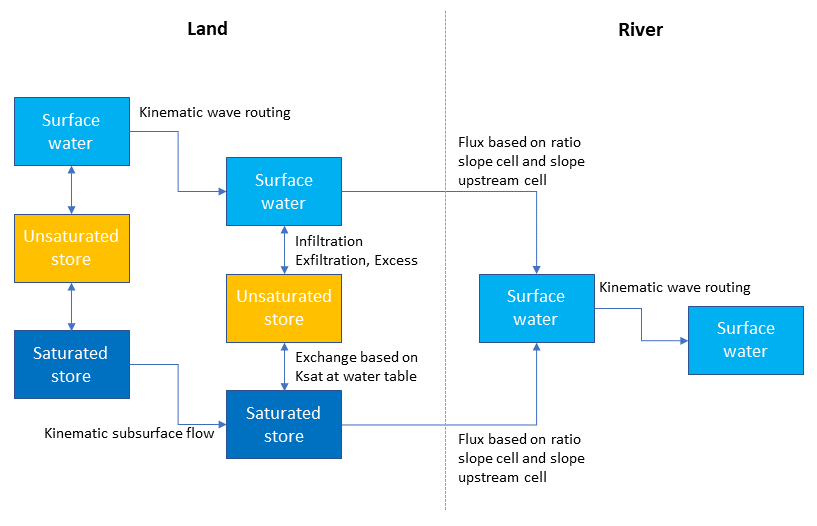
The figure below shows the stores and fluxes in the model in terms of internal variable names.

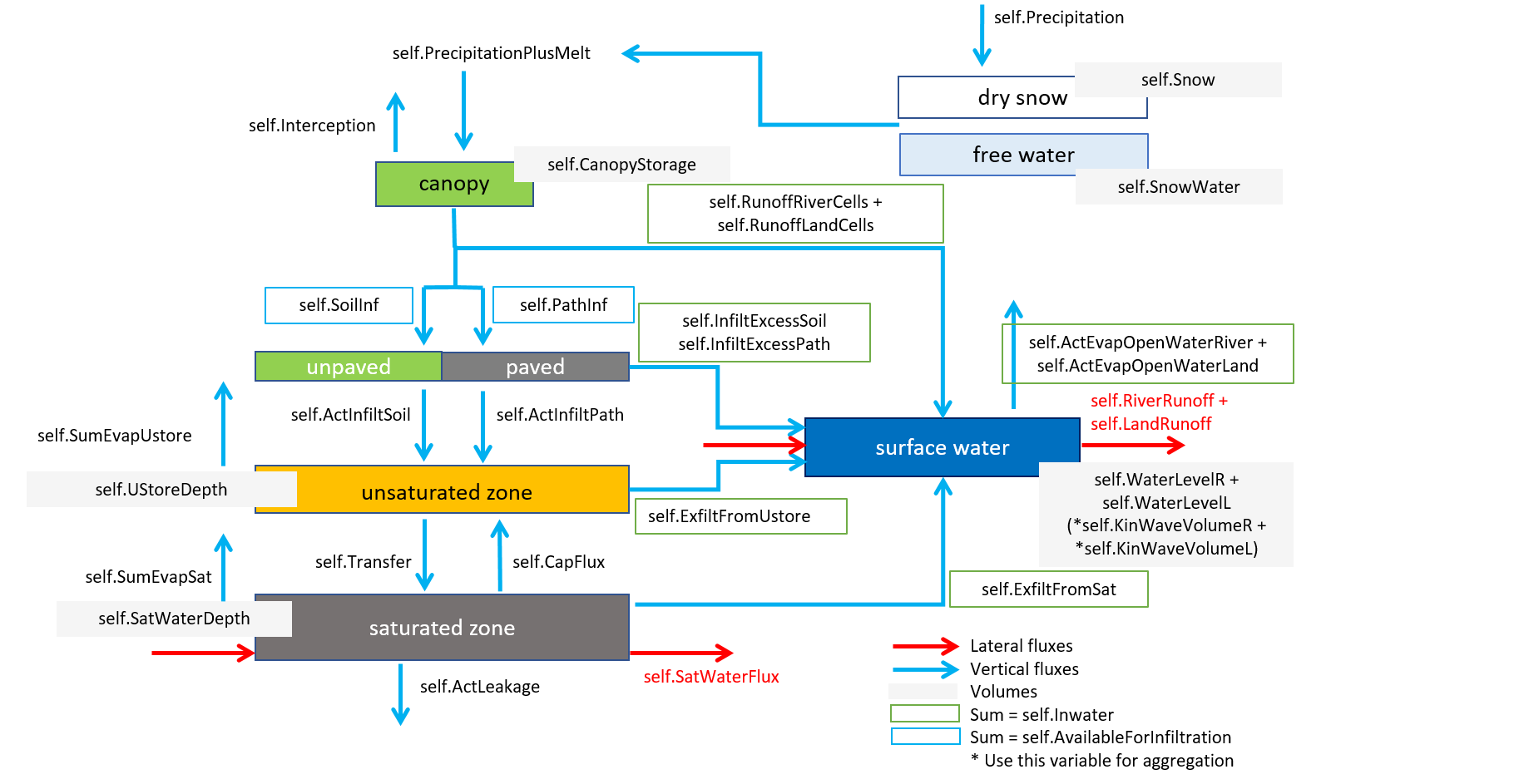
Complete wflow scheme.

Processing of meteorological forcing data

Although the model has been setup to do as little data processing as possible it includes an option to apply an altitude correction to the temperature inputs. The three squares below demonstrate the principle.

wflow_sbm takes the correction grid as input and applies this to the input temperature. The correction grid has to be made outside of the model. The correction grid is optional.

The temperature correction map is specified in the model section of the ini file:

[model]
TemperatureCorrectionMap=NameOfTheMap

If the entry is not in the file the correction will not be applied

Wflow_sbm model parameters

The list below shows the most important model parameters

CanopyGapFraction

Gash interception model parameter [-]: the free throughfall coefficient.

EoverR

Gash interception model parameter. Ratio of average wet canopy evaporation rate over average precipitation rate.

SoilThickness

Maximum soil depth [mm]

SoilMinThickness

Minimum soil depth [mm]

MaxLeakage

Maximum leakage [mm/day]. Leakage is lost to the model. Usually only used for i.e. linking to a dedicated groundwater model. Normally set to zero in all other cases.

KsatVer

Vertical saturated conductivity [mm/day] of the store at the surface. The M parameter determines how this decreases with depth.

KsatHorFrac

A multiplication factor [-] applied to KsatVer for the horizontal saturated conductivity used for computing lateral subsurface flow. This parameter compensates for anisotropy, small scale KsatVer measurement (small soil core) that do not represent larger scale hydraulic conductivity, and model resolution (in reality smaller (hillslope) flow length scales).

InfiltCapPath

Infiltration capacity [mm/day] of the compacted soil (or paved area) fraction of each gridcell.

InfiltCapSoil

Infiltration capacity [mm/day] of the non-compacted soil fraction (unpaved area) of each gridcell.

M

Soil parameter M [mm] determines the decrease of vertical saturated conductivity with depth. Usually between 20 and 2000.

MaxCanopyStorage

Canopy storage [mm]. Used in the Gash interception model.

N and N_River

Manning N parameter for the kinematic wave function for overland and river flow. Higher valuesdampen the discharge peak.

PathFrac

Fraction of compacted area per gridcell [-].

RootingDepth

Rooting depth of the vegetation [mm].

thetaR

Residual water content [mm/mm].

thetaS

Water content at saturation [mm/mm].

c

Brooks-Corey power coefficient [-] based on the pore size distribution index \(\lambda\), used for computing vertical unsaturated flow.

Note

If SoilThickness and SoilMinThickness are not equal, wflow_sbm will scale SoilThickness based on the topographic wetness index.

Implementation of SoilThickness scaling:

# soil thickness based on topographic wetness index (see Environmental modelling: finding simplicity in complexity)
# 1: calculate wetness index
# 2: Scale the soil thickness (now actually a max) based on the index, also apply a minimum soil thickness
WI = pcr.ln(
    pcr.accuflux(self.TopoLdd, 1) / self.landSlope
)  # Topographic wetnesss index. Scale WI by zone/subcatchment assuming these are also geological units
WIMax = pcr.areamaximum(WI, self.TopoId) * WIMaxScale
self.SoilThickness = pcr.max(
    pcr.min(self.SoilThickness, (WI / WIMax) * self.SoilThickness),
    self.SoilMinThickness,
)

Calibrating the wflow_sbm model

Introduction

As with all hydrological models calibration is needed for optimal performance. We have calibrated different wflow_sbm models using simple shell scripts and command-line parameters to multiply selected model parameters and evaluate the results later.

Parameters

SoilThickness

Increasing the soil depth and thus the storage capacity of the soil will decrease the outflow.

M

Once the depth of the soil has been set (e.g. for different land-use types) the M parameter is the most important variable in calibrating the model. The decay of the conductivity with depth controls the baseflow resession and part of the stormflow curve.

N and N_River

The Manning N parameter controls the shape of the hydrograph (the peak parts). In general it is advised to set N to realistic values for the rivers, for the land phase higher values are usually needed.

KsatVer and KsatHorFrac

Increasing KsatVer and or KsatHorFrac will lower the hydrograph (baseflow) and flatten the peaks. The latter also depend on the shape of the catchment.

References

• Vertessy, R.A. and Elsenbeer, H., 1999, Distributed modelling of storm flow generation in an Amazonian rainforest catchment: effects of model parameterization, Water Resources Research, vol. 35, no. 7, pp. 2173–2187.

• Brooks, R., and Corey, T., 1964, Hydraulic properties of porous media, Hydrology Papers, Colorado State University, 24, doi:10.13031/2013. 40684.

• Chow, V., Maidment, D. and Mays, L., 1988, Applied Hydrology. McGraw-Hill Book Company, New York.

• Finnegan, N.J., Roe, G., Montgomery, D.R., and Hallet, B., 2005, Controls on the channel width of rivers: Implications for modeling fluvial incision of bedrock, Geology, v. 33; no. 3; p. 229–232; doi: 10.1130/G21171.1.

• Wigmosta, M. S., L. J. Lane, J. D. Tagestad, and A. M. Coleman, 2009, Hydrologic and erosion models to assess land use and management practices affecting soil erosion, Journal of Hydrologic Engineering, 14(1), 27-41.

wflow_sbm module documentation