The wflow_routing Model¶

Introduction¶

The wflow routing module uses the pcraster kinematic wave to route water over a DEM. By adding a bankfull level and a floodplainwidth to the configuration the model can also include estimated flow over a floodplain. In addition, simple reservoirs can be configured.

Method¶

A simple river profile is defined using a river width a bankfull heigth and a floodplainwidth. A schematic drawing is shown in the figure below.

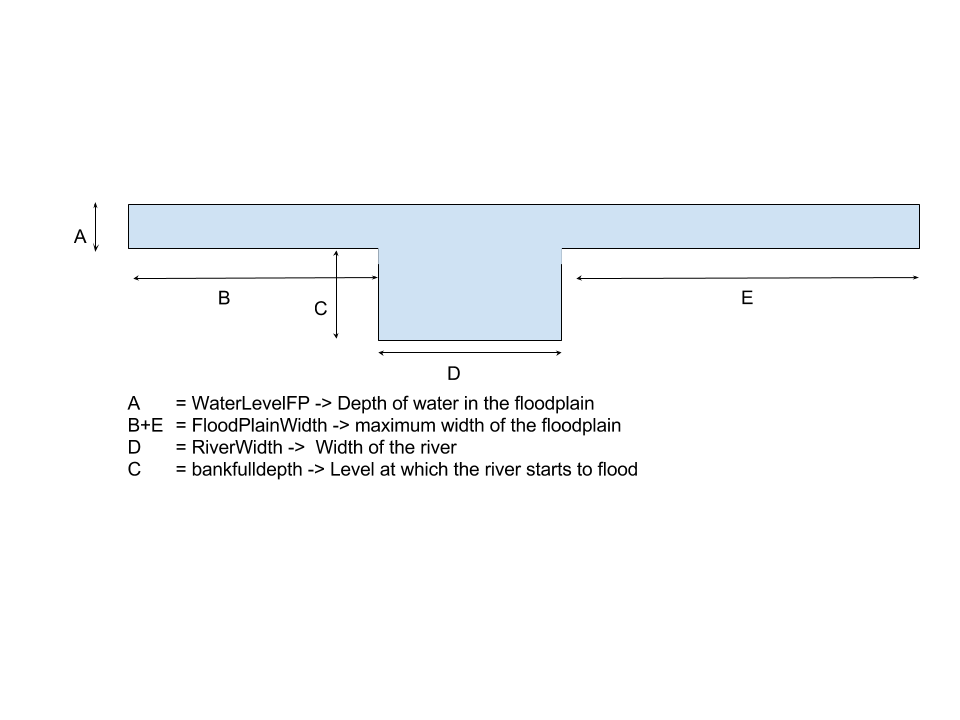
First the maximum bankfull flow for each cell is determined using:

\[Q_b = (\frac{H_{b}}{\alpha{_{ch}}} * Bw)^{1/\beta}\]

Next the channel flow is determined by taking the mimumm value of the total flow and the maximum banfull flow and the floodplain flow is determined by subtracting the bankfull flow from the total flow.

In normal conditions (below bankfull), the waterlevel in the river is determined as follows:

\[H_{ch} = \alpha{_{ch}} {Q_{ch}}^{\beta}/ Bw\]

Where \(H_{ch}\) is the water level for the channel, \(\alpha{_{ch}}\) is the kinematic wave coefficient for the channel, \(Q_{ch}\) is the discharge in the channel and \(Bw\) is the width of the river.

If the water level is above bankfull the water level on the floodplains is calculated as follows:

\[H_{fp} = \alpha{_{fp}} {Q_{fp}}^{\beta}/ (Bw + P_{fp})\]

where \(H_{ch}\) is the water level on the floodplain, \(Q_{fp}\) is the discharge on the floodplain and \(P_{fp}\) is the wetted perimiter of the floodplain and \(\alpha{_{fp}}\) is the kinematic wave coefficient for the floodplain,

The wetted perimiter of the channel, \(P_{ch}\), is determined by:

\[P_{ch} = 2.0 H_{ch} + Bw\]

The wetted perimiter of the floodplain is defined as follows:

\[ \begin{align}\begin{aligned}N = max(0.0001,1.0/(1.0 + exp(-c * H_{fp}) - 0.5) * 2.0\\P_{fp} = N W_{fp}\end{aligned}\end{align} \]

This first equation defines the upper half of an S or sigmoid curve and will return values between 0.001 and 1.0. The c parameter defines the sharpness of the function, a high value of c will turn this into a step-wise function while a low value will make the function more smooth. The default value for c = 0.5. For example, with this default value a floodplain level of 1m will result in an N value of 0.25 and 2m will return 0.46. In the second equation this fraction is multiplied with the maximum floodplain width \(W_{fp}\).

The \(\alpha\) for the channel and floodplain are calculated as follows:

\[ \begin{align}\begin{aligned}\alpha_{ch} = (n_{ch}/\sqrt{slope})^\beta P_{ch}^{(2.0 / 3.0)\beta}\\\alpha_{fp} = (n_{fp}/\sqrt{slope})^\beta P_{fp}^{(2.0 / 3.0)\beta}\end{aligned}\end{align} \]

In which slope is the slope of the river bed and floodplain and \(n_{ch}\) and \(n_{fp}\) represent the manning’s n for the channel and floodplain respectively.

A compound \(\alpha_{total}\) is estimated by first calculating a compound n value \(n_{total}\):

\[ \begin{align}\begin{aligned}n_{total} = (P_{ch}/P_{total} n_{ch}^{3/2} + P_{fp}/P_{total} n_{fp}^{3/2})^{2/3}\\\alpha_{total} = (n_{total}/\sqrt{slope})^\beta (P_{fp} + P_{ch})^{(2.0 / 3.0)\beta}\end{aligned}\end{align} \]

The \(\alpha_{total}\) is used in the pcraster kinematic function to get the discharge for the next timestep.

The code is implemented in the updateRunoff attribute of the model class as follows:

self.Qbankfull = pow(self.bankFull/self.AlphaCh * self.Bw,1.0/self.Beta)
self.Qchannel = min(self.SurfaceRunoff,self.Qbankfull)
self.floodcells  = boolean(ifthenelse(self.WaterLevelCH > self.bankFull, boolean(1), boolean(0)))
self.Qfloodplain = max(0.0,self.SurfaceRunoff - self.Qbankfull)

self.WaterLevelCH = self.AlphaCh * pow(self.Qchannel, self.Beta) / (self.Bw)
self.WaterLevelFP = ifthenelse(self.River,self.AlphaFP * pow(self.Qfloodplain, self.Beta) / (self.Bw + self.Pfp),0.0)
self.WaterLevel = self.WaterLevelCH + self.WaterLevelFP

# Determine Qtot as a check
self.Qtot = pow(self.WaterLevelCH/self.AlphaCh * self.Bw,1.0/self.Beta) + pow(self.WaterLevelFP/self.AlphaFP * (self.Pfp + self.Bw),1.0/self.Beta)
# wetted perimeter (m)
self.Pch = self.wetPerimiterCH(self.WaterLevelCH,self.Bw)
self.Pfp = ifthenelse(self.River,self.wetPerimiterFP(self.WaterLevelFP,self.floodPlainWidth,sharpness=self.floodPlainDist),0.0)

# Alpha
self.WetPComb = self.Pch + self.Pfp
self.Ncombined = (self.Pch/self.WetPComb*self.N**1.5 + self.Pfp/self.WetPComb*self.NFloodPlain**1.5)**(2./3.)
self.AlpTermFP = pow((self.NFloodPlain / (sqrt(self.SlopeDCL))), self.Beta)
self.AlpTermComb = pow((self.Ncombined / (sqrt(self.SlopeDCL))), self.Beta)
self.AlphaFP = self.AlpTermFP * pow(self.Pfp, self.AlpPow)
self.AlphaCh = self.AlpTerm * pow(self.Pch, self.AlpPow)
self.Alpha = ifthenelse(self.River,self.AlpTermComb * pow(self.Pch + self.Pfp, self.AlpPow),self.AlphaCh)
self.OldKinWaveVolume = self.KinWaveVolume
self.KinWaveVolume = (self.WaterLevelCH * self.Bw * self.DCL) + (self.WaterLevelFP * (self.Pfp + self.Bw) * self.DCL)

Reservoirs¶

Simple reservoirs can be included within the kinematic wave routing by supplying a map with the locations of the reservoirs in which each reservoir has a unique id. Furthermore a set of lookuptables must be defined linking the reservoir-id’s to reservoir characteristics:

ResTargetFullFrac.tbl - Target fraction full (of max storage) for the reservoir: number between 0 and 1
ResTargetMinFrac.tbl - Target minimum full fraction (of max storage). Number between 01 and 1 < ResTargetFullFrac
ResMaxVolume.tbl - Maximum reservoir storage (above which water is spilled) [m^3]
ResDemand.tbl - Water demand on the reservoir (all combined) m^3/s
ResMaxRelease.tbl - Maximum Q that can be released if below spillway [m^3/s]

By default the reservoirs are not included in the model. To include them put the following lines in the .ini file of the model.

[modelparameters]
# Add this if you want to model reservoirs
ReserVoirLocs=staticmaps/wflow_reservoirlocs.map,staticmap,0.0,0
ResTargetFullFrac=intbl/ResTargetFullFrac.tbl,tbl,0.8,0,staticmaps/wflow_reservoirlocs.map
ResTargetMinFrac=intbl/ResTargetMinFrac.tbl,tbl,0.4,0,staticmaps/wflow_reservoirlocs.map
ResMaxVolume=intbl/ResMaxVolume.tbl,tbl,0.0,0,staticmaps/wflow_reservoirlocs.map
ResMaxRelease=intbl/ResMaxRelease.tbl,tbl,1.0,0,staticmaps/wflow_reservoirlocs.map
ResDemand=intbl/ResDemand.tbl,tblmonthlyclim,1.0,0,staticmaps/wflow_reservoirlocs.map

In the above example most values are fixed thought the year, only the demand is given per month of the year.

Configuration¶

The default name for the file is wflow_routing.ini.

Subcatchment flow¶

Normally the the kinematic wave is continuous throughout the model. By using the the SubCatchFlowOnly entry in the model section of the ini file all flow is at the subcatchment only and no flow is transferred from one subcatchment to another. This can be handy when connecting the result of the model to a water allocation model such as Ribasim.

Example:

[model]
SubCatchFlowOnly = 1

Forcing data¶

The model needs one set of forcing data: IW (water entering the model for each cell in mm). The name of the mapstack is can be defined in the ini file. By default it is inmaps/IW

See below for an example:

[inputmapstacks]
Inwater = /run_default/outmaps/IW
Inflow = /inmaps/IF

[run]
starttime = 1995-01-31 00:00:00
endtime = 1995-02-28 00:00:00
timestepsecs = 86400
reinit = 0

[model]
modeltype = routing
AnnualDischarge = 2290
Alpha = 120
WIMaxScale = 0.8
Tslice = 1
UpdMaxDist = 300000.0
reinit = 1
fewsrun = 0
OverWriteInit = 0
updating = 0
updateFile = no_set
sCatch = 0
intbl = intbl
timestepsecs = 86400
MaxUpdMult = 1.3
MinUpdMult = 0.7
UpFrac = 0.8
SubCatchFlowOnly = 0
wflow_subcatch = staticmaps/wflow_subcatch.map
wflow_dem = staticmaps/wflow_dem.map
wflow_ldd = staticmaps/wflow_ldd.map
wflow_river = staticmaps/wflow_river.map
wflow_riverlength = staticmaps/wflow_riverlength.map
wflow_riverlength_fact = staticmaps/wflow_riverlength_fact.map
wflow_gauges = staticmaps/wflow_gauges.map
wflow_inflow = staticmaps/wflow_inflow.map
wflow_riverwidth = staticmaps/wflow_riverwidth.map
wflow_floodplainwidth = staticmaps/wflow_floodplainwidth.map
wflow_bankfulldepth = staticmaps/wflow_bankfulldepth.map
wflow_landuse = staticmaps/wflow_landuse.map
wflow_soil = staticmaps/wflow_soil.map

[framework]
outputformat = 1
debug = 0
netcdfinput = None
netcdfoutput = None
netcdfstaticoutput = None
netcdfstaticinput = None
EPSG = EPSG:4326

[layout]
sizeinmetres = 0

[outputmaps]
self.SurfaceRunoff = _run
self.Qfloodplain = _qfp
self.Qchannel = _qch
self.Qbankfull = _qbnk
self.WaterLevelFP = _levfp
self.WaterLevelCH = _levch
self.InwaterMM = _IW
self.floodcells = fcel
self.Qtot = QQQ
self.Pch = ch
self.Pfp = fp
self.Alpha = al
self.AlphaCh = alch
self.AlphaFP = alfp
self.Ncombined = nc
self.MassBalKinWave = wat

[outputcsv_0]
samplemap = None

[outputtss_0]
samplemap = None

A description of the implementation of the kinematic wave is given on the pcraster website at http://pcraster.geo.uu.nl/pcraster/4.0.2/doc/manual/op_kinematic.html

In addition to the settings in the ini file you need to give the model additional maps or lookuptables in the staticmaps or intbl directories:

Lookup tables¶

N.tbl:: Manning’s N for all no-river cells. Defaults to 0.072
N_River.tbl:: Manning’s N for the river cells. Defaults to 0.036
N_FloodPlain.tbl:: Manning’s N for the floodplain. A floodplain is always linked to a river cell. Defaults to 2* N of the river
ResDemand.tbl:: Lookup table of demand (\(m^3/s\)) for reservoir locations.
ResMaxRelease.tbl:: Lookup table of maximum release capcity (\(m^3/s\)) for reservoir locations.
ResMaxVolume.tbl:: Lookup table of reservoi maximum volume (\(m^3\)) for reservoir locations.
ResTargetFullFrac:: Lookup table of the target maximum full fraction (0-1) (\(m^3/s\)) for reservoir locations.
ResTargetMinFrac:: Lookup table of the target minimum full fraction (0-1) (\(m^3/s\)) for reservoir locations.

As with all models the lookup tables can be replaced by a map with the same name (but with the .map extension) in the staticmaps directory.

staticmaps¶

wflow_subcatch.map:: Map of the subcatchment in the area. Usually shared with the hydrological model
wflow_dem.map:: The digital elevation model. Usually shared with the hydrological model
wflow_ldd.map:: The D8 local drainage network.
wflow_river.map:: Definition of the river cells.
wflow_riverlength.map:: Optional map that defines the actual legth of the river in each cell.
wflow_riverlength_fact.map:: Optional map that defines a multiplication factor for the river length in each cell.
wflow_gauges.map:: Map of river gauges that can be used in outputting timeseries
wflow_inflow.map:: Optional map of inflow points into the surface water. Limited testing.
wflow_riverwidth.map:: Optional map of the width of the river for each river cell.
wflow_floodplainwidth.map:: Optional map of the width of the floodplain for each river cell.
wflow_bankfulldepth.map:: Optional map of the level at which the river starts to flood and water will also be conducted over the floodplain.
wflow_floodplaindist.map:: Optional map that defines the the relation between bankfulldepth and the floodplaindepth. Default = 0.5
wflow_landuse.map:: Required map of landuse/land cover. This map is used in the lookup tables to relate parameters to landuse/landcover. Usually shared with the hydrological model
wflow_soil.map:: Required map of soil type. Usually shared with the hydrological model

initial conditions¶

The model needs the following files with initial conditions:

WaterLevelCH:: Water level in the channel or the grid-cell water level for non-river cells.
WaterLevelFP:: Water level in the floodplain
SurfaceRunoff:: Discharge in each grid-cell
ReservoirVolume:: Volume of each reservoir in \(m^3\)

The total waterlevel is obtained by adding the two water levels.